Hello Everyone, This is Nikhil Nandam back with yet another article on machine learning, this time being Linear Regression. So let's jump right in!
To understand Linear Regression, we need to first understand the about the class of machine learning models that Linear Regression belongs.
As the name suggests, Linear Regression falls under Regression category of machine learning models.
Regression
The class of machine learning models where the target value(s) are continuous (i.e) not discrete like classification models. Typically, the target values are numeric.
What is a linear model?
A linear model is a sum of weighted variables that predicts a target output value given an input data instance.
Linear Regression
Linear Regression is an example of linear model.
Each input instance must have numerical features and the generalised form of input instance - feature vector is shown below.
$$ x = (x_0, x_1, x_2, ... , x_n) $$
where \(x_0, x_1, ... , x_n\) are numerical input features of the instance.
The output is predicted using a formula that generalised below.
$$ \hat{y} = \hat{w_0}x_0 + \hat{w_1}x_1 + \hat{w_2}x_2 + ... \hat{w_n}x_n + \hat{b} $$
where \(\hat{y}\) represents predicted target value and \(w_0, w_1, ... , w_n\) are called feature weights / model coefficients. \(\hat{b}\) is a constant bias term or intercept.
Compare this general formula to the general formula of a straight line.
$$ y = mx + c $$
where
$$ m = \hat{w} = (w_0, w_1, w_2, ... , w_n) $$
$$ x = (x_0, x_1, x_2, ... , x_n) $$
$$ c = \hat{b} $$
The main task of the model is to estimate \(\hat{w}\) and \(\hat{b}\)
$$ \hat{y_i} = w_{i} \cdot x_{i} + \hat{b} $$
$$ \hat{y} = \hat{w} \cdot x + \hat{b} $$
Estimating Model Parameters
- The model parameters \(\hat{w}\) and \(\hat{b}\), as discussed above, can be estimated using many different ways.
- The learning algorithm finds the parameters that optimise an objective function, typically to minimise some kind of loss function of the predicted target values vs. the actual target values.
Least-Squares Linear Regression(Ordinary Least-Squares)
The least-squares linear regression model finds \(\hat{w}\) and \(\hat{b}\) that minimises the squared error of the model.
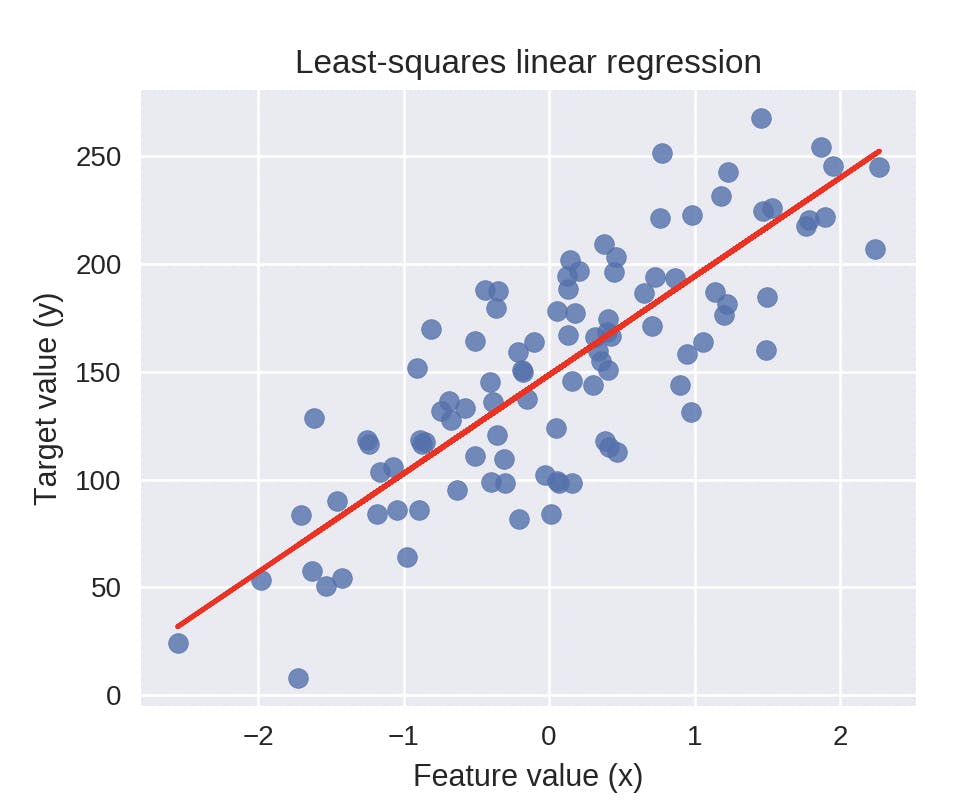
The objective of the model is to minimise the squared error the model which is calculated using the formula below.
$$ SquaredError = \sum_{i = 1} ^ {n} (y_i - \hat{y_i}) ^ 2 $$
where \(y_i\) is the actual target value and \(\hat{y_i}\) is the predicted target value.
Sci-kit Learn Module Implementation
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
linear_model = LinearRegression()
linear_model.fit(X_train, y_train)
The model's coefficient (i.e slope) and intercept are stored as model attributes and can be shown using the code below.
print('linear model coefficient (w) = {}'.format(linear_model.coef_))
print('linear model intercept (b) = {}'.format(linear_model.intercept_))
The model performance is calculated using the R-Squared Score also called coefficient of determination of the prediction.
R-Squared Score
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\) where \(u\) is the residual sum of squares and \(v\) is the total sum of squares.
$$ u = \sum_{i=1}^n (y_i - \hat{y}_i)^2 $$
and
$$ v = \sum_{i=1}^n (y_i - \sum_{i=1}^n\frac{y_i}{n})^2 $$
The R-squared score of the model on the training-set data and the test-set data can be found out using the code shown below.
print('R-squared score (training): {:.3f}'.format(linear_model.score(X_train, y_train)))
print('R-squared score (test): {:.3f}'.format(linear_model.score(X_test, y_test)))
Advantages and Disadvantages
Advantages
- Linear Regression is simple to understand and to implement.
- No parameter tuning is required.
- Linear Regression models though seem simplistic, can very effectively be generalised to data that have lots of input features.
Disadvantages
- Linear Regression models makes strong assumption about the data. Precisely, Linear Regression models assumes a linear relationship between dependent and independent variables.
- Linear Regression models perform very poorly on highly complex data where the input features are not linearly dependent on the target value.
That's it for now guys! Hope you learned something new through this article. Leave your feedback and suggestions in the comments down below. Happy Learning!!! 😉
