Hello everyone, so this is Nikhil Nandam back yet with another article on various evaluation metrics of a trained model. There are various metrics to evaluate the performance of our model on new previously unseen data and I am going to elaborate on the most commonly used metrics for binary classification. Without any further delay, let’s get started.
So starting off with
What is an evaluation metric?
An evaluation metric is some calculation that is done when the model predicts the labels(target class) for a small percentage of available data(test_set) to gain insight on how well the trained model is at predicting the right labels for the data.
It is necessary as it lets us decide whether further tuning of the model parameters is required or not.
Terminology
There are some terms that are really needed to proceed further.
True_Positive(TP): A data instance is categorised as True_Positive when the model predicts the label of the instance to be positive and the actual label of the instance is also positive.
False_Positive(FP): A data instance is categorised as False_Positive when the model predicts the label of the instance to be positive but the actual label of the instance is negative.
False_Negative(FN): A data instance is categorised as False_Negative when the model predicts the label of the instance to be negative but the actual label of the instance is positive.
True_Negative(TN): A data instance is categorised as True_Negative when the model predicts the label of the instance to be negative and the actual label of the instance is also negative. Again these terms are used only in the context of classification models, not regression. Below is an image that represents this precisely.
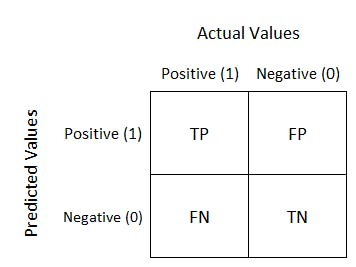The above image is matrix which is called a confusion matrix.
Now with these terminology out of the way, let's proceed further.
Accuracy
The first evaluation metric we are going to discuss is accuracy. Accuracy is defined as the ratio of correctly labelled instances to the to the total number of instances. More precisely, the ratio of the sum of true_positives(TP) plus true_negatives(TN) over the total number of instances.
$$ accuracy = \frac{TP + TN}{No. of Instances} $$
Or more precisely,
$$ accuracy = \frac{TP + TN}{TP + FP + FN + TN} $$
Precision
The next metric is precision. Precision is the ratio of number of correctly predicted positives over the total number of instances that were predicted positive. More precisely, the ratio of true_positives(TP) over the sum of true_positives(TP) and false_positives(FP).
$$ precision = \frac{TP}{TP + FP} $$
Recall
Another metric is called recall. Recall is the ratio of number of correctly predicted positives over the total number of instances that were actually positive. More precisely, the ratio of true_positives(TP) over the sum of true_positives(TP) and false_negatives(FN).
$$ recall = \frac{TP}{TP + FN} $$
Note the very slight difference between precision and recall. It takes some time to wrap your head around this concept.
You might be thinking "I might simply use accuracy why bother about confusing metrics like precision and recall”. I’ll give you a convincing example of how and when they are actually useful.
Suppose you belong the crime branch and using some magic have been able to create a machine learning model that can predict whether a person is a criminal or not; where a criminal is labelled as positive(1) and an innocent is labelled(0) according to the model. You need to make a trade-off between 2 situations that arise.
To not let a criminal escape by any means: If you want your model to correctly identify every criminal as a criminal, you should tune the model in a way that no person is labelled innocent when he is actually a criminal, implying the false_negatives should be as minimum as possible. So tuning the model to improve its recall is essential.
To not punish an innocent person by any means: If you want your model to not misidentify an innocent as a criminal, you should tune the model in a way that no person is labelled criminal when he is actually an innocent, implying the false_positives should be as minimum as possible. So tuning the model to improve its precision is essential.
F1-Score
The final metric is based on the metrics discussed above. F1-Score conveys the balance between precision and recall.
$$ f_{1} = 2 * \frac{precision * recall}{precision + recall} $$
also calculated by
$$ f_{1} = \frac{TP}{TP + \frac{1}{2}(FP + FN)} $$
Calculating various metrics using Sklearn
Below are the code snippets with an example used to calculate various metrics from sklearn.
#importing phase
from sklearn.neighbors import KNeighborsClassier
from sklearn.model_selection import train_test_split
#train_test_split_phase
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0, test_size=0.33)
model = KNeighborsClassifier(n_neighbors=3) # creating the model
model.fit(X_train, y_train) # fitting the model on training data
predictions = model.predict(X_test) #predicting labels for test data
Confusion Matrix
from sklearn.metrics import confusion_matrix
print(confusion_matrix(y_test, predictions)) # confusion matrix
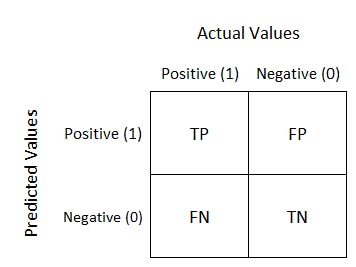
This produces an output similar to the image below
where the numbers correspond to the values mapped to the matrix below.
Classification Report
A classification report can be used to calculate precision, recall and f1-score at the same time using classification_report function in sklearn.metrics module.
from sklearn.metrics import classification_report
# classification_report
print(classification_report(y_test, predictions))
This produces an output similar to the one shown below.
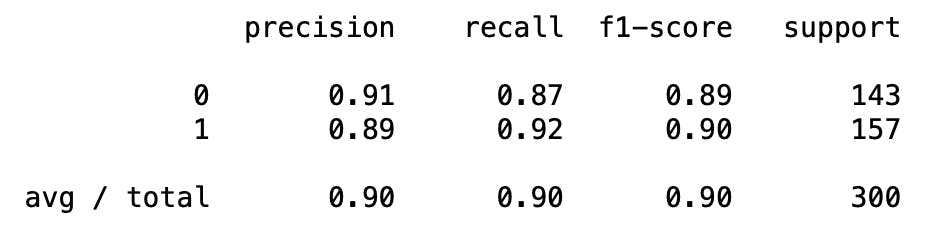
That's it for now guys! Hope you find this article insightful.
Please leave a like if you liked it and do let me know your thoughts, feedback and suggestions in the comments down below. Happy learning and have a great day! 😁😄
